Role

PhD student (2010-2014)

Topic

Statistical Signal Processing and Adaptive Filter Theory

Application

Optical Communication receiver design

Contributions

Proposed (i) 2 novel adaptive learning algorithms, namely, CWDAML and adaptive CWDA for long-haul optical communication receiver design, and (ii) an all-optical filter design for intensity-modulated direct-detected radio-over-fiber receivers, used in broadband wireless optical access networks.

CWDAML and Adaptive CWDA Algorithm

Overview

Thesis

Digital and optical compensation of signal impairments for optical communication receivers

Summary

This is my Ph.D. dissertation work. I proposed and implemented 2 novel adaptive learning algorithms for real-time-series data prediction and classification using modified linear and logistic regression techniques. It was applied to long-haul optical communication receiver application.

  • CWDAML: A complex-weighted, decision-aided, maximum-likelihood, joint phase and frequency estimator for intradyne coherent receivers
  • Adaptive CWDA: A low complexity, low cycle-slip probability, format-independent carrier estimator with adaptive filter length for linear- and nonlinear-noise impaired channels

Our algorithms (i) predict the channel parameters or the impairment value (i.e., noise) introduced in the optical fiber using statistical modelling techniques and then (ii) classify the received data (bits, i.e., 1s and 0s) at the receiver using regression and adaptive learning techniques.

We provide below on this page, a brief explanation of the (i) prediction/classification problem addressed by CWDAML and adaptive CWDA algorithms and (ii) the Matlab source codes simulating the prformance of these two algorithms. For brevity, mathematical derivations, proofs, and algorithm analysis, are skipped and interested readers are referred to my thesis for details.

Furthermore in my PhD, I had proposed an optical filter design for simultaneous signal equalization, chirp modulation, and single-sideband filtering in intensity-modulated direct-detection (IMDD) radio-over-fiber (RoF) receivers, used for broadband wireless optical access networks. This is an ingenious, highly efficient, all-optical-domain signal processing technique, with no need for additional digital signal processing. It solves multiple issues simultaneously, namely, constrained modulation bandwidth, limited transmission distance, and radio frequency signal fading. The effectiveness of our optical filter design was proved experimentally. Interested readers are referred to my thesis for the mathematical operating principles and for further explanation of our proposed optical filter design.

Repository

The repository consists of the following:

  • CWDAML - Matlab codes
  • Adaptive CWDA - Matlab Codes

Info

Long haul optical communication systems aim for bit rates per channel in excess of 100 Gb/s as the next interface rates are geared toward 400 Gb/s and 1 Tb/s1,2. Increasing the transmission capacity, to service the growth of data traffic, at a fixed optical amplification bandwidth requires increasing the spectral efficiency.

Coherent detection with multilevel modulation promises superior spectral efficiency, receiver sensitivity, and transmission distance compared to noncoherent systems3, and enables the attainment of Shannon’s capacity with the use of coding such as Turbo codes4,5,6.

Current interest lies in intradyne coherent detection using a free running local oscillator (LO) laser, followed by sampling with high-speed analog-to-digital converter (ADC), and execution of carrier estimation in digital signal processing (DSP) modules7.

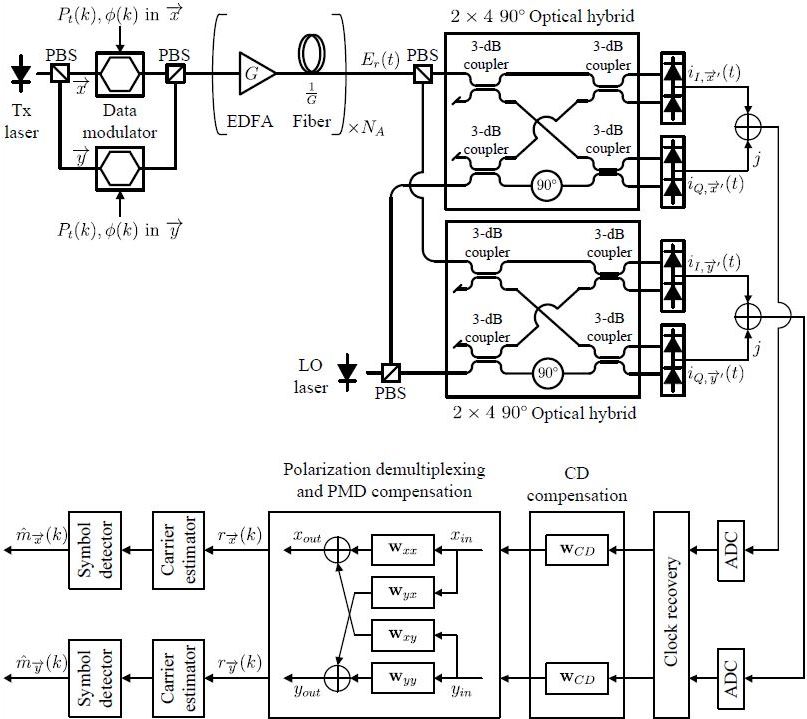
coh_sys
Polarization multiplexed coherent optical communication receiver. Tx: transmitter.

Consider a dual-polarization optical transmission system with an intradyne receiver shown in the figure above. The transmission system can be divided into transmitter, channel, and receiver portions.

At the transmitter, amplitude and phase of the transmitter laser is modulated by a symbol sequence (i.e., data). To minimize bit errors due to symbol errors at the receiver, careful bits-to-symbol mapping is needed. The bits-to-symbol mapping for several differentially encoded 4-, 8-, and 16-ary discrete-point constellations which use both field quadratures is shown below.

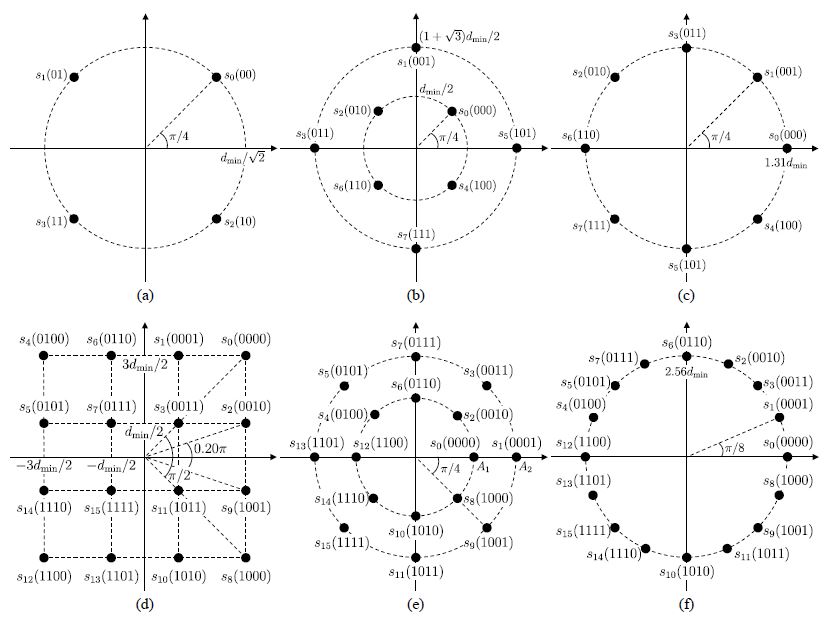
const

Signal constellation and bits-to-symbol mapping for (a) QPSK, (b) 8-QAM, (c) 8-PSK, (d) 16-QAM, (e) 16-Star, and (f) 16-PSK.

The modulated optical field is then transmitted through multiple spans of standard single mode fiber with periodic optical amplification to compensate for fiber attenuation loss. Optical amplifiers produce amplified spontaneous emission (ASE) noise which degrades the signal-to-noise ratio (SNR) of the amplified signal. ASE noise is modelled as zero-mean, circularly symmetric complex Gaussian. Typically, long-haul amplified transmission systems are ASE noise limited since ASE noise is generally much larger than shot noise and thermal noise8,9.

A key difference between optical fiber and other transmission media is the presence of nonlinear effects. The dominant nonlinear impairment in fiber is the Kerr nonlinearity, where the refractive index of silica fiber vary with the signal power. Interaction of signal and ASE noise with the Kerr effect generates self-phase-modulation (SPM) induced nonlinear phase noise10. Nonlinear phase noise impairs the performance of phase-modulated optical systems11.

The receiver comprises of four key subsystems, namely,

  1. optical hybrid downconverter which linearly maps the optical field into electrical signals,
  2. ADC which quantizes the analog signal into a set of discrete values,
  3. DSP modules which compensate for transmission impairments, and
  4. the symbol detector which performs coherent symbol detection.

The LO laser at the receiver is free running, in contrast to a homodyne coherent detection where the LO need to be phase- and frequency-locked to the optical carrier of the received optical signal. The angular frequency offset between the transmitter and LO lasers results in a frequency offset \(\Delta f\) impairment in the received signal. Additionally, the receved signal is impaired by phase noise, modelled as Wiener process, arising from nonzero linewidth \(\Delta\nu\) of the Lorentzian line-shaped transmitter and LO lasers.

Key DSP modules comprise of

  1. clock recovery,
  2. chromatic dispersion compensation,
  3. polarization demultiplexing and polarization-mode dispersion (PMD) compensation, and
  4. carrier phase and frequency estimation.

In principle, all linear impairments can be compensated ideally using digital filters12. A more detailed explanation of the complete coherent transmission system is described in the thesis.

In this PhD contribution, we focused on the carrier estimator and symbol detector blocks, which involves carrier phase and frequency prediction followed by classification of the received symbol sequence. At high SNR, the optimum symbol-by-symbol receiver structure consists of a carrier estimator followed by a coherent symbol detector, as illustrated by the last two blocks in the optical communication receiver above13. Two adaptive learning algorithms were developed to accomplish this task, namely,

  1. Complex Weighted Decision Aided Maximum Likelihood (CWDAML), and
  2. Adaptive Complex Weighted Decision Aided (adaptive CWDA).

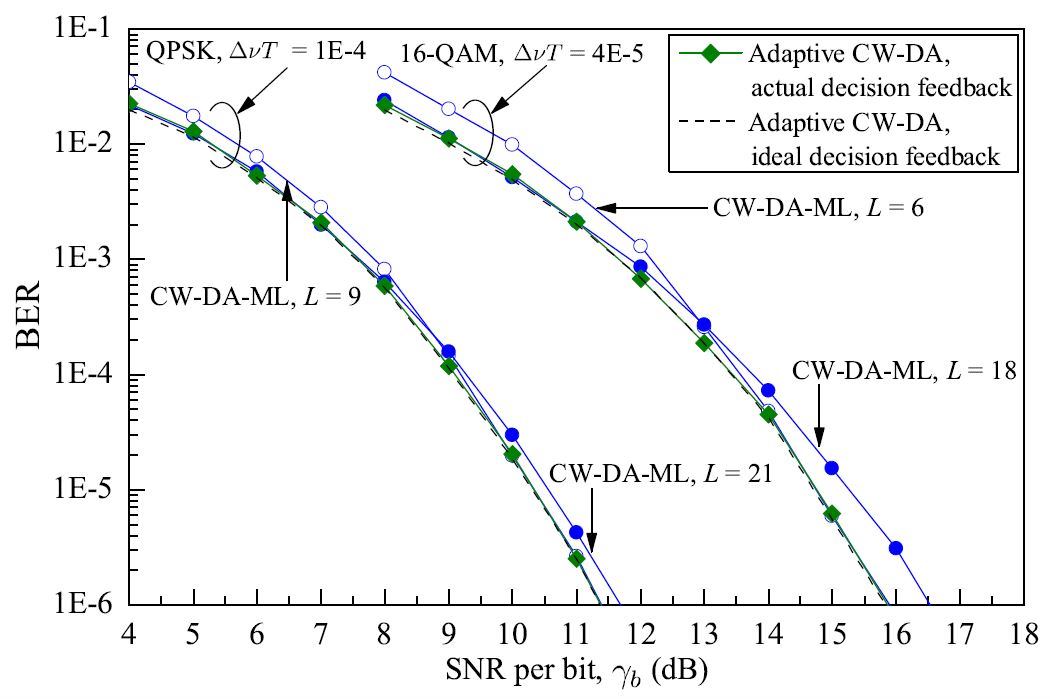
The repository contains Matlab codes to simulate CWDAML and adptive CWDA algorithm for M-ary phase-shift keying (MPSK) and M-ary quadrature amplitude modulation (MQAM) formats. The simulations consists of transmitter, fiber optic transmission medium, additive Gaussian noise, laser phase noise, nonlinear phase noise, frequency offset between transmitter and LO lasers, IQ receiver, ADC quantization effect, and baseband digital signal processing comprising CWDAML or adaptive CWDA algorithm. Accuracy of symbol prediction and classification is measured in terms of bit-error rate (BER). The Matlab codes produces BER vs SNR graph (i.e., waterfall curves).

Next, we provide brief overview of the two algorithms and operating examples of the Matlab simulation codes. Chapter 3 and 4 of the thesis describes the development of our two adaptive algorithms in greater detail.

CWDAML14

Interest in a decision aided estimator lies in its maximum likelihood derivation, and its near optimum maximum likelihood carier estimation at high and medium SNR15. CWDAML is a decision-aided least-squares based estimator, which achieves fast carrier acquisition, complete frequency estimation range, low SNR operability, requires no phase unwrapping, reliably tracks time-varying frequency, and is format transparent. Additionally, a pilot-assisted CWDAML estimator was demonstrated to require low pilot overhead.

Operating example:

  1. Only parameters in the main files need to be modified.
  2. Main file will call all other files which are function files.
  3. Simulation will take several minutes to complete.
  4. A "Results" folder must be created in the same directory as the rest of the code files to store the results at the end of the simulation.

Some suggested settings:

  1. For 4PSK, with linear phase noise and frequency offset impairment 
     main file: "CWDAML_and_AdaptiveCWDA\CWDAML\Linear phase noise and frequency offset\Batch_file.m"
 rp.SNR_begin = 6; %starting SNR for graph plotting
 rp.M = 4; %modulation order 
 rp.format = 'PSK'; %modulation format
 symbolRate = 28e9; %symbols/s
 FL = 15; %filter length
 LSR = 11.2e6/symbolRate; %Laser linewidth(Hz)/Symbol_Rate
 FSR = 2.8e9/symbolRate; %Frequency offset(Hz)/Symbol_Rate
 value = CWDAML_MPSK(rp);
  2. For 16-QAM, with linear phase noise and frequency offset impairment 
     main file: "CWDAML_and_AdaptiveCWDA\CWDAML\Linear phase noise and frequency offset\Batch_file.m"
 rp.SNR_begin = 8; %starting SNR for graph plotting
 rp.M = 16; %modulation order 
 rp.format = 'QAM'; %modulation format
 symbolRate = 28e9; %symbols/s
 FL = 15; %filter length
 LSR = 1.12e6/symbolRate; %Laser linewidth(Hz)/Symbol_Rate 
 FSR = 2.8e9/symbolRate; %Frequency offset(Hz)/Symbol_Rate
 value = CWDAML_MQAM(rp);
  3. For 4-PSK, with nonlinear phase noise impairment 
     main file: "CWDAML_and_AdaptiveCWDA\CWDAML\Nonlinear phase noise\NL_Batch_file.m"
 rp.M = 4; %modulation order
 rp.format = 'PSK'; %modulation format
 rp.bit_rate = log2(rp.M)*28e9; %bit rate, units: bits/s
 LSR = 200e3/28e9; %200kHz laser linewidth(Hz)/Symbol_Rate
 FSR = 0; %frequency offset(Hz)/Symbol_Rate
 LP = (-10:2:10).'; %range of launch power(dBm)
 rp.filter_length = 21; %filter length
 rp.training_length = 100; %training_length
 rp.freq_est_length = 4e3; %No_sent_symbols to be used for frequency estimation    
 value = NL_CW_recursiveW_DAML_MPSK(rp);

Adaptive CWDA16

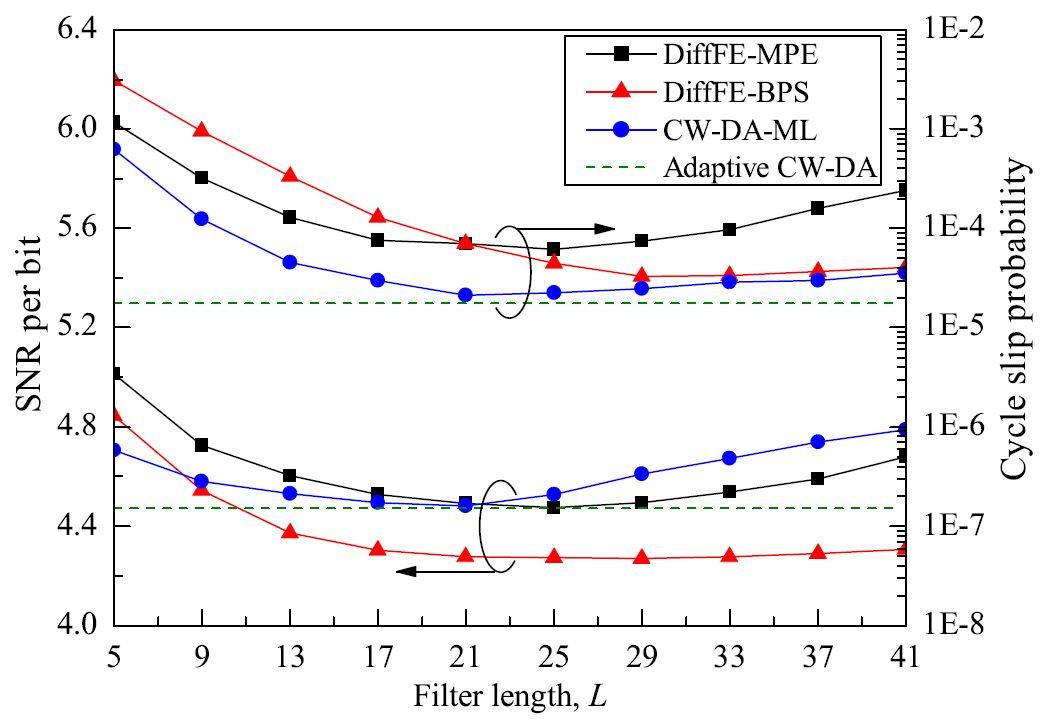
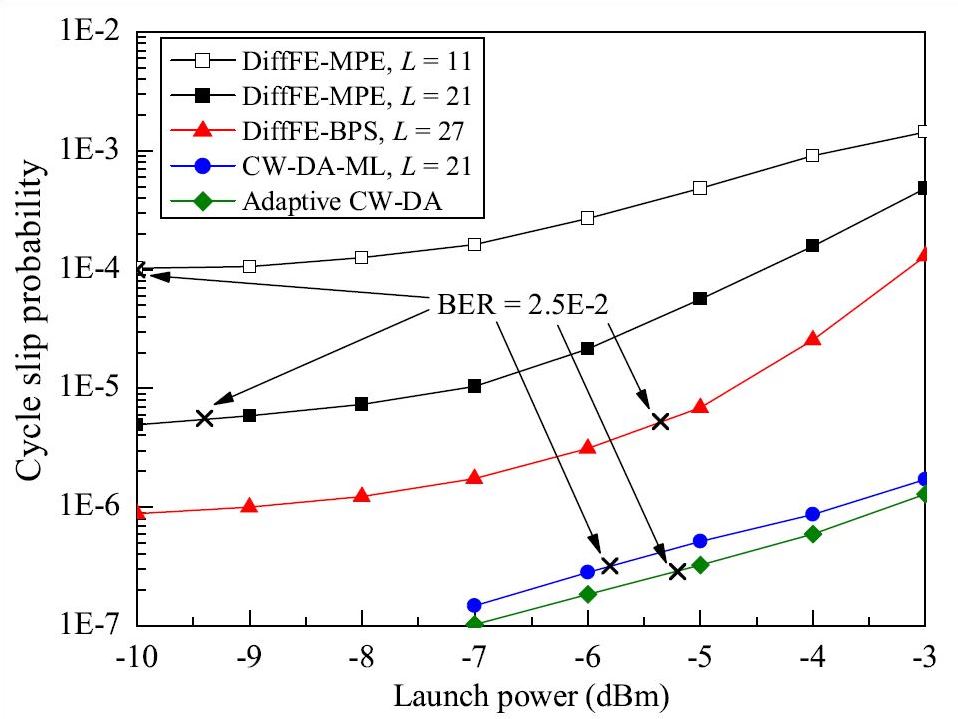
Progress towards a fully reconfigurable optical network demands carrier estimators with adaptive filter length to optimize the BER. The filter length of a carrier estimator also affects the cycle slip probability besides the BER. Considering that forward error correction (FEC) codes are not robust to burst errors and cycle slips, filter-length optimization is necessary to avoid spectral-efficiency reduction in pilot-assisted systems and potential system failures in differential encoding systems. Hence, adaptive CWDA estimator with an effective filter length that automatically adapts according to the SNR, laser-linewidth-per-symbol-rate \(\Delta\nu T\), nonlinear phase noise, and modulation format was derived. It can operate in a set-and-forget mode as it requires no a priori system statistics and no preset parameters. Adaptive CWDA estimator achieves a lower cycle slip probability and a greater nonlinear phase noise tolerance than CWDAML estimator. Reduced complexity, due to the two-tap structure, makes adaptive CWDA estimator favorable for practical implementation.

Operating example:

  1. Only parameters in the main files need to be modified.
  2. Main file will call all other files which are function files.
  3. Simulation will take several minutes to complete.
  4. A "Results" folder must be created in the same directory as the rest of the code files to store the results at the end of the simulation.

Some suggested settings:

  1. For 4PSK, with linear phase noise and frequency offset impairment 
     main file: "CWDAML_and_AdaptiveCWDA\Adaptive CWDA\Linear phase noise and frequency offset\Batch_file.m"
 rp.SNR_begin = 6; %starting SNR for graph plotting
 rp.M = 4; %modulation order 
 rp.format = 'PSK'; %modulation format
 symbolRate = 28e9; %symbols/s
 LSR = 11.2e6/symbolRate; %Laser linewidth(Hz)/Symbol_Rate
 FSR = 2.8e9/symbolRate; %Frequency offset(Hz)/Symbol_Rate
 value = Adaptive_CWDA_MPSK(rp);
  2. For 16-QAM, with linear phase noise and frequency offset impairment 
     main file: "CWDAML_and_AdaptiveCWDA\Adaptive CWDA\Linear phase noise and frequency offset\Batch_file.m"
 rp.SNR_begin = 8; %starting SNR for graph plotting
 rp.M = 16; %modulation order 
 rp.format = 'QAM'; %modulation format
 symbolRate = 28e9; %symbols/s
 LSR = 1.12e6/symbolRate; %Laser linewidth(Hz)/Symbol_Rate 
 FSR = 2.8e9/symbolRate; %Frequency offset(Hz)/Symbol_Rate
 value = Adaptive_CWDA_MQAM(rp);
  3. For 4-PSK, with nonlinear phase noise impairment 
     main file: "CWDAML_and_AdaptiveCWDA\Adaptive CWDA\Nonlinear phase noise\NL_Batch_file.m"
 rp.M = 4; %modulation order
 rp.format = 'PSK'; %modulation format
 rp.bit_rate = log2(rp.M)*28e9; %bit rate, units: bits/s
 LSR = 200e3/28e9; %200kHz laser linewidth(Hz)/Symbol_Rate
 FSR = 0; %frequency offset(Hz)/Symbol_Rate
 LP = (-10:2:10).'; %range of launch power(dBm)
 rp.training_length = 300; %training_length
 rp.freq_est_length = 4e3; %No_sent_symbols to be used for frequency estimation   
 value = NL_Adaptive_CWDA_MPSK(rp);

References

  1. P. J. Winzer, “Beyond 100G ethernet,” IEEE Commun. Mag., vol. 48, no. 7, pp. 26–30, Jul. 2010. ↩

  2. A. H. Gnauck, P. J. Winzer, S. Chandrasekhar, X. Liu, B. Zhu, and D. W. Peckham, “Spectrally efficient long-haul WDM transmission using 224-Gb/s polarization-multiplexed 16-QAM,” J. Lightw. Technol., vol. 29, no. 4, pp. 373–377, Feb. 2011. ↩

  3. L. G. Kazovsky, G. Kalogerakis, and W.-T. Shaw, “Homodyne phase-shift keying systems: past challenges and future opportunities,” J. Lightw. Technol., vol. 24, no. 12, pp. 4876–4884, Dec. 2006. ↩

  4. C. Berrou, A. Glavieux, and P. Thitimajshima, “Near Shannon limit error correcting coding and decoding: turbo-codes,” in Proc. ICC, Geneva, Switzerland, 1993, pp. 1064–1070. ↩

  5. S.-Y. Chung, G. D. Forney, Jr., T. J. Richardson, and R. Urbanke, “On the design of low-density parity-check codes within 0.0045 db of the Shannon limit,” IEEE Commun. Lett., vol. 5, no. 2, pp. 58–60, Feb. 2001. ↩

  6. C. Berrou, “The ten-year-old turbo codes are entering into service,” IEEE Commun. Mag., vol. 41, no. 8, pp. 110–116, Aug. 2003. ↩

  7. F. Derr, “Coherent optical QPSK intradyne system: concept and digital receiver realization,” J. Lightw. Technol., vol. 10, no. 9, pp. 1290–1296, Sep. 1992. ↩

  8. E. Ip, A. P. T. Lau, D. J. F. Barros, and J. M. Kahn, “Coherent detection in optical fiber systems,” Opt. Exp., vol. 16, no. 2, pp. 753–791, Jan. 2008. ↩

  9. A. Yariv, “Signal-to-noise considerations in fiber links with periodic or distributed optical amplification,” Opt. Lett., vol. 15, no. 19, pp. 1064–1066, Oct. 1990. ↩

  10. J. P. Gordon and L. F. Mollenauer, “Phase noise in photonic communications systems using linear amplifiers,” Opt. Lett., vol. 15, no. 23, pp. 1351–3, Dec. 1990. ↩

  11. H. Kim and A. H. Gnauck, “Experimental investigation of the performance limitation of DPSK systems due to nonlinear phase noise,” IEEE Photon. Technol. Lett., vol. 15, no. 2, pp. 320–322, Feb. 2003. ↩

  12. J. G. Proakis, Digital Communications, 5th ed. New York: McGraw-Hill, 2008. ↩

  13. P.-Y. Kam, S. S. Ng, and T. S. Ng, “Optimum symbol-by-symbol detection of uncoded digital data over the Gaussian channel with unknown carrier phase,” IEEE Trans. Commun., vol. 42, no. 8, pp. 2543–2552, Aug. 1994. ↩

  14. A. Meiyappan, P.-Y. Kam, and H. Kim, “On decision aided carrier phase and frequency offset estimation in coherent optical receivers,” J. Lightw. Technol., vol. 31, no. 13, pp. 2055–2069, Jul. 2013. ↩

  15. R. D. Gaudenzi, T. Garde, and V. Vanghi, “Performance analysis of decision directed maximum-likelihood phase estimators for M-PSK modulated signals,” IEEE Trans. Commun., vol. 43, no. 12, pp. 3090–3100, Dec. 1995. ↩

  16. A. Meiyappan, H. Kim, and P.-Y. Kam, “A low-complexity, low-cycle-slip probability,format-independent carrier estimator with adaptive filter length,” J. Lightw. Technol., vol. 31, no. 23, pp. 3806–3812, Dec. 2013. ↩

Updated:

Leave a comment